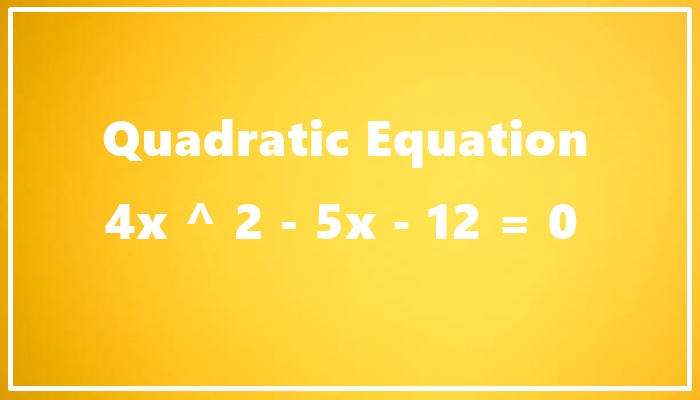Quadratic equations form the cornerstone of algebra and are integral to various branches of mathematics and science. The equation 4x ^ 2 – 5x – 12 = 0 exemplifies the standard form of a quadratic equation ax2+bx+c=0where a, and c are constants and x represents the variable. This particular equation is intriguing due to its coefficients and the solutions it yields.
Method of Solution 4x ^ 2 – 5x – 12 = 0
The quadratic equation can be solved using several methods, each with its unique approach and utility. The most common techniques are factorization, completing the square, and the quadratic formula. Factorization involves rewriting the quadratic as a product of two binomials while completing the square transforming the equation into a perfect square. However, the most universally applicable method, especially for equations that are difficult to factorize, is the quadratic formula:
x=−b
±b2−4ac2a
In our case, with 4x ^ 2 – 5x – 12 = 0, the coefficients are ,
, and .

Calculation
Applying the quadratic formula to our equation, we substitute the values of
,
, and as follows:
x=−(−5)±(−5)2−4⋅4⋅(−12)2⋅4
x=5±25+1928
x=5±2178
This simplifies to two solutions:
x1=5+2178
, x
2=5−2178
These solutions are the roots of the equation, representing the values of
for which the equation holds.
Significance and Applications
Quadratic equations are pivotal in various scientific and engineering disciplines. The roots of these equations can represent real-world quantities like the time of flight or maximum height in projectile motion, optimal solutions in economics, or points of equilibrium in chemical reactions. Understanding the nature of these solutions, whether real, complex, or repeated, provides insights into the behavior of the system being studied.
Real-World Example
In physics, the trajectory of a projectile is often modeled by a quadratic equation, where the solutions can indicate the time at which the projectile reaches a certain height. Similarly, in economics, the profit maximization problem can be modeled as a quadratic equation, where the roots indicate maximum or minimum profit points.
Must Read:
Conclusion
The quadratic equation 4x ^ 2 – 5x – 12 = 0 is more than a mere mathematical expression; it is a gateway to understanding complex phenomena in the natural and social sciences. By delving into its solutions, we uncover patterns and principles fundamental to various fields, illustrating the profound interconnectedness of mathematics with the world around us.